mbleven – A fast algorithm for bounded edit distance

Author:

Fujimoto Seiji

Published:

2012-03-01

Copyright:

This document has been placed in the public domain.

mbleven is a fast algorithm to compute k-bounded Levenshtein distance. In general, it’s one of the fastest algorithm for cases where the bound parameter is small (\(k < 3\)).

1. How fast is it?

To illustrate the performance characteristic, I conducted a benchmark test that compares mbleven and the Wagner-Fischer algorithm.

The measurement was done by count the time each algorithm takes to process 4 million binary strings. Here is the graph that shows the result (on Intel Core i3-4010U with GCC 6.3.0):

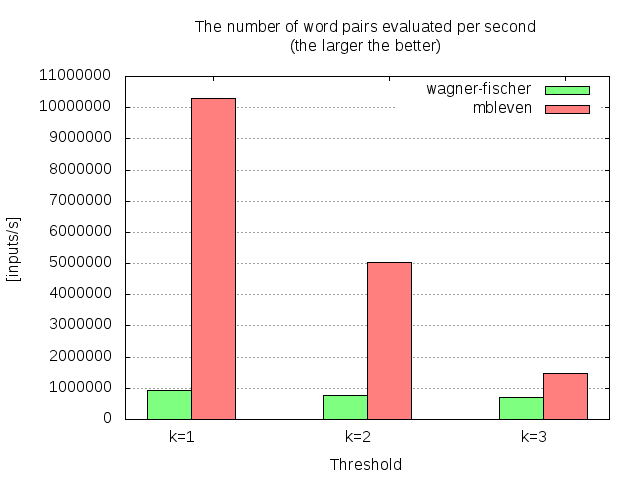
The benchmark program is available from mbleven-benchmark.c. To run this program:

$ cc -O2 -o mbleven-benchmark mbleven-benchmark.c
$ ./mbleven-benchmark

2. Implementations

There are several implementations available.

• mbleven is the reference implementation written in Python. This implementation also supports Damerau-Levenshtein distance.

• distance contains a C implementation (See fast_comp() function).

• polyleven contains another C implementation.

3. How it works

mbleven is a hypothesis-based algorithm, which means that it solves the edit distance problem by testing a collection of hypotheses.

Suppose you are trying to compute the distance between \(S\) and \(T\) under the constraint \(k = 1\). The mbleven algorithm first enumerates all the edit operations that are possible under the threshold \(k\):

1. Can an insertion transform \(S\) to \(T\)?

2. Can a deletion transform \(S\) to \(T\)?

3. Can a substitution transform \(S\) to \(T\)?

Then, mbleven checks each hypothesis one by one to find out if any of them holds true.

As explained later, each hypothesis can be verified in \(O(n)\) time using \(O(1)\) space, so it can run quite faster than the common algorithms that require \(O(n^2)\) time.

3.1. Efficient Pruning

One important aspect of mbleven is very efficient pruning of search space. In particular, we can reject most of hypotheses just by looking at the length of input strings.

Consider the task of computing the edit distance between S = ‘foo’ and T = ‘bar’ under the constraint \(k = 1\). We can immediately see that a substitution is the only hypothesis that we need to check.

Why? It’s because ‘foo’ and ‘bar’ have the same string lengths (3 chars), so operations such as “one insertion” or “one deletion” can’t convert one into another.

We can expand this argument to other cases as well. If S = ‘foo’ and T = ‘fo’ with \(k=2\), we only need to check “one deletion + one substitution”. If S = ‘foobar’ and T = ‘bar’ with \(k=3\), we just need to test “three deletions”.

3.2. Verification Algorithm

As mentioned above, each hypothesis can be verified in \(O(n)\) time. The following code shows how the verification can be done:

def check_model(s, t, model):
    m = len(s)
    n = len(t)
    k = len(model)
    i, j, c = 0, 0, 0
    while (i < m) and (j < n):
        if s[i] != t[j]:
            if k <= c:
                return c + 1
            if model[c] == 'd':  # deletion
                i += 1
            elif model[c] == 'i':  # insertion
                j += 1
            elif model[c] == 'r':  # replacement/substitution
                i += 1
                j += 1
            c += 1
        else:
            i += 1
            j += 1
    return c + (m - i) + (n - j)

This function returns the number of the operations it consumed to convert \(S\) into \(T\). If the return value is greater than \(k\), it means that the specified model cannot transform \(S\) into \(T\).

As you can see, each iteration of the while loop increments i or j, so the main loop will break after at most \(n + m\) steps. Thus, this function runs in linear time to the length of the input strings.