Find similar pairs of DNA sequences¶
- Author:
Fujimoto Seiji
- Publish:
2022-11-26
- Copyright:
This document has been placed in the public domain.
1. Introduction¶
Suppose that you have bio dataset that contains 10k DNA sequences. For research purpose, you want to find every pair in the dataset that differ only by one character (base-pair). How would you implement it?
Let’s restate this problem in a more formal manner:
Given a dataset containing N DNA sequences, find all pairs where Levenshtein distance is at most 1.
This article explores several solutions for this problem.
2. How to solve it?¶
2.1. Naive solution¶
If \(N\) is small, you can just compute all the combination of the DNA sequences. Here is what I have in mind:
from itertools import combinations
from polyleven import levenshtein
# dataset = ["AGCT", "AGTT", ...]
def naive(dataset):
for dna1, dna2 in combinations(dataset, 2):
if levenshtein(dna1, dna2) < 2:
print(dna1, dna2)
Since we need to compute \(N(N-1) \over 2\) pairs, this solution consumes \(O(N^2)\) time.
2.2. Faster solution (with FastSS)¶
The computation time for the previous solution increases quadratically as \(N\) gets bigger. It will be not feasible at a certain data size.
The common way to handle this issue is to introduce a clever index structure that allows to find similar entries quickly. One such data structure is FastSS [Bocek2007].
The basic idea is:
If two strings is similar enough, they should have a common substring. For example, AGTCA and AGTCG look very similar, exactly because they share the same prefix AGTC.
This means that, theoretically, you can parittion entries by their substrings. In this scheme, AGTCA will be in the same group with AGTCG, but TTTGT won’t.
This partitioning will make the task easy, because you only need to evaluate combinations within each group, which contains only a small subset of the original dataset.
For details, please read the referenced paper. Here is the simple implementation of this idea:
from collections import defaultdict
from itertools import combinations
from polyleven import levenshtein
def make_index(word, max_dist):
res = set()
length = len(word)
for dist in range(min(max_dist, length) + 1):
variants = combinations(word, length - dist)
for variant in variants:
res.add(''.join(variant))
return res
def fastss(dataset):
groups = defaultdict(set)
for dna in dataset:
for key in make_index(dna, 1):
groups[key].add(dna)
for grp in groups.values():
for dna1, dna2 in combinations(grp, 2):
if levenshtein(dna1, dna2) < 2:
print(dna1, dna2)
3. Benchmark¶
The following graph shows how much time each solution requires to process a dataset of size N.
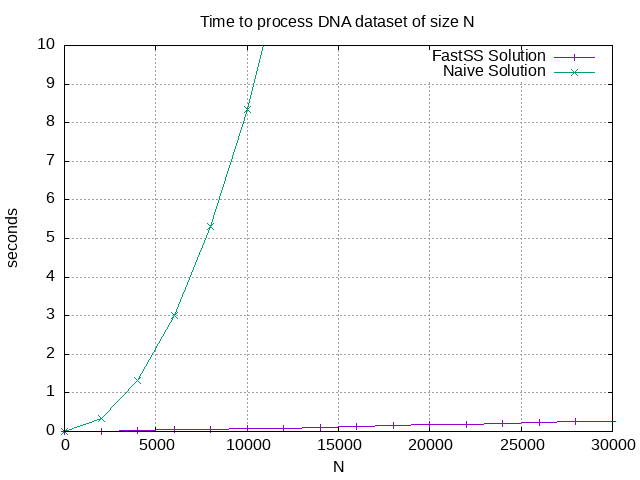
You can see that using a search index reduces the computation time quite significantly.
4. References¶
fujimotos/kindna includes a full implementation of the faster solution.